As early as 1945 a computational device known as a neural network (a.k.a. a multi-layered perceptron network) was invented. It was patterned after the networks formed by neuron cells in animal brains [see figure 3]. In 1975 a technique called backpropagation was developed that significantly advanced the learning capability of these networks. They were “trained” on a sample of input data (observations), then could be used to make predictions about future and/or out-of-sample data.
Neurons in the first layer were connected by “synaptic weights” to the data inputs. The inputs could be any number of things, e.g. one pixel in an image, the status of a square on a chessboard, or financial data of a company. These neurons would multiply the input values by the synaptic weights and sum them. If the sum exceeded some threshold value the neuron would fire and take on a value of 1 for neurons in the second layer, otherwise it would not fire and produce a value of 0. Neurons in the second layer were connected to the first via another set of synaptic weights and would fire by the same rules, and so on to the 3rd, 4th, layers etc. until culminating in an output layer. Training examples were fed to the model one at a time. The network’s outputs were compared against the known results to evaluate errors. These were used to adjust the weights in the network via the aforementioned backpropagation technique: weights that contributed to the error were reduced while weights contributing to a correct answer were increased. With each example, the network followed the error gradient downhill (gradient descent). The training stopped when no further improvements were made.

Figure 3: A hypothetical neural network with an input layer, 1 hidden layer, and an output layer, by Glosser.ca (CC BY-SA) via Wikimedia Commons.
Neural Networks exploded onto the scene in the 1980’s and stunned us with how well they would learn. More than that, they had a “life-like” feel as we could watch the network improve with each additional training sample, then become stuck for several iterations. Suddenly the proverbial “lightbulb would go on” and the network would begin improving again. We could literally watch the weights change as the network learned. In 1984 the movie “The Terminator” was released featuring a fearsome and intelligent cyborg character, played by Arnold Schwarzenegger, with a neural network for a brain. It was sent back from the future where a computerized defense network, Skynet, had “got smart” and virtually annihilated all humanity!
The hysteria did not last, however. The trouble was that while neural networks did well on certain problems, on others they failed miserably. Also, they would converge to a locally optimal solution but often not a global one. There they would remain stuck only with random perturbations as a way out – a generally hopeless proposition in a difficult problem. Even when they did well learning the in-sample training set data, they would sometimes generalize poorly. It was not understood why neural nets succeeded at times and failed at others.
In the 1990’s significant progress was made understanding the mathematics of the model complexity of neural networks and other computer models and the field of learning theory really emerged. It was realized that most of the challenging problems were highly non-linear, having many minima, and any gradient descent type approach would be vulnerable to becoming stuck in one. So, a new kind of computer model was developed called the support vector machine. This model rendered the learning problem as a convex optimization problem – so that it had only one minima and a globally optimal result could always be found. There were two keys to the support vector machine’s success: first it did something called margin-maximization which reduced overfitting, and, second, it allowed computer scientists to use their familiarity with the problem to choose an appropriate kernel – a function which mapped the data from the input feature space into a smooth, convex space. Like a smooth bowl-shaped valley, one could follow the gradient downhill to a global solution. It was a way of introducing domain knowledge into the model to reduce the amount of twisting and turning the machine had to do to fit the data. Bayesian techniques offered a similar helping hand by allowing their designers to incorporate a “guess”, called the prior, of what the model parameters might look like. If the machine only needed to tweak this guess a little bit to come up with a posterior, the model could be interpreted as a simple correction to the prior. If it had to make large changes, that was a complex model, and, would negatively impact expected generalization ability – in a quantifiable way. This latter point was the second half of the secret sauce of machine learning – allowing clever people to incorporate as much domain knowledge as possible into the problem so the learning task was rendered as simple as possible for the machine. Simpler tasks required less contortion on the part of the machine and resulted in models with lower complexity. SVM’s, as they became known, along with Bayesian approaches were all the rage and quickly established machine learning records for predictive accuracy on standard datasets. Indeed, the mantra of machine learning was: “have the computer solve the simplest problem possible”.

Figure 4: A kernel, , maps data from an input space, where it is difficult to find a function that correctly classifies the red and blue dots, to a feature space where they are easily separable – from StackOverflow.com.
It would not take long before the science of controlling complexity set in with the neural net folks – and the success in learning that came with it. They took the complexity concepts back to the drawing board with neural networks and came out with a new and greatly improved model called a convolutional neural network. It was like the earlier neural nets but had specialized kinds of hidden layers known as convolutional and pooling layers (among others). Convolutional layers significantly reduced the complexity of the network by limiting neurons connectivity to only a nearby region of inputs, called the “receptive field”, while also capturing symmetries in data – like translational invariance. For example, a vertical line in the upper right hand corner of the visual field is still a vertical line if it lies in the lower left corner. The pooling layer neurons could perform functions like “max pooling” on their receptive fields. They simplified the network in the sense that they would only pass along the most likely result downstream to subsequent layers. For example, if one neuron fires, weakly indicating a possible vertical line, but, another neuron fires strongly indicating a definite corner, then only the latter information is passed onto the next layer of the network [see Figure 5].

Figure 5: Illustration of the function of max pooling neurons in a pooling layer of a convolutional neural network. By Aphex34 [CC BY-SA 4.0] via Wikimedia Commons
The idea for this structure came from studies of the visual cortex of cats and monkeys. As such, convolutional neural networks were extremely successful at enabling machines to recognize images. They quickly established many records on standardized datasets for image recognition and to this day continue to be the dominant model of choice for this kind of task. Computer vision is on par with human object recognition ability when the human subject is given a limited amount of time to recognize the image. A mystery that was never solved was: how did the visual cortex figure out its own structure.
Interestingly, however, when it comes to more difficult images, humans can perform something called top-down reasoning which computers cannot replicate. Sometimes humans will look at an image, not recognize it immediately, then start using a confluence of contextual information and more to think about what the image might be. When ample time is given for humans to exploit this capability we exhibit superior image recognition capability. Just think back to the last time we were requested to type in a string of disguised characters to validate that we were, indeed, human! This is the basis for CAPTCHA: Completely Automated Public Turing test to tell Computers and Humans Apart. [see Figure 6].

Figure 6: An example of a reCAPTCHA challenge from 2007, containing the words “following finding”. The waviness and horizontal stroke were added to increase the difficulty of breaking the CAPTCHA with a computer program. Image and caption by B Maurer at Wikipedia
While machine learning was focused on quantifying and managing the complexity of models for learning, the dual concept of the Kolmogorov complexity had already been developed in 1965 in the field of information theory. The idea was to find the shortest description possible of a string of data. So, if we generate a random number by selecting digits at random without end, we might get something like this:
5.549135834587334303374615345173953462379773633128928793.6846590704…
and so on to infinity. An infinite string of digits generated in this manner cannot be abbreviated. That is, there is no simpler description of the number than an infinitely long string. The number is said to have infinite Kolmogorov complexity, and is analogous to a machine learning model with infinite VC dimension. On the other hand, another similar looking number, , extends out to infinity:
3.14159265358979323846264338327950288419716939937510582097494459230…
never terminating and never repeating, yet, it can be expressed in a much more compact form. For example, we can write a very simple program to perform a series approximation of to arbitrary accuracy using the Madhava-Leibniz series (from Wikipedia):

So, has a very small Kolmogorov complexity, or minimum description length (MDL). This example illustrates the abstract, and far-from-obvious nature of complexity. But, also, illustrates a point about understanding: when we understand something, we can describe it in simple terms. We can break it down. The formula, while very compact, acts as a blueprint for constructing a meaningful, infinitely long number. Mathematicians understand . Similar examples of massive data compression abound, and some, like the Mandelbrot set, may seem biologically inspired [see Figure 7].

Figure 7: This image illustrates part of the Mandelbrot set (fractal). Simply storing the 24-bit color of each pixel in this image would require 1.62 million bits, but a small computer program can reproduce these 1.62 million bits using the definition of the Mandelbrot set and the coordinates of the corners of the image. Thus, the Kolmogorov complexity of the raw file encoding this bitmap is much less than 1.62 million bits in any pragmatic model of computation. Image and caption By Reguiieee via Wikimedia Commons
Perhaps life, though, has managed to solve the ultimate demonstration of MDL – the DNA molecule itself! Indeed, this molecule, some 3 billion nucleotides (C, A, G, or T) long in humans, encodes an organism of some 3 billion-billion-billion ( ) amino acids. A compression of about a billion-billion to 1 (
) amino acids. A compression of about a billion-billion to 1 (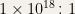 ). Even including possible epigenetic factors as sources of additional blueprint information (epigenetic tags are thought to affect about 1% of genes in mammals), the amount of compression is mind boggling. John von Neuman pioneered an algorithmic view of DNA, like this, in 1948 in his work on cellular automata. Biologists know, for instance, that the nucleotide sequences: “TAG”, “TAA”, and “TGA” act as stop codons (Hat tip Douglas Hoftstadter in Gödel, Escher, Bach: An Eternal Golden Braid) in DNA and signal the end of a protein sequence. More recently, the field of Evolutionary Developmental Biology (a.k.a. evo-devo) has encouraged this view:
). Even including possible epigenetic factors as sources of additional blueprint information (epigenetic tags are thought to affect about 1% of genes in mammals), the amount of compression is mind boggling. John von Neuman pioneered an algorithmic view of DNA, like this, in 1948 in his work on cellular automata. Biologists know, for instance, that the nucleotide sequences: “TAG”, “TAA”, and “TGA” act as stop codons (Hat tip Douglas Hoftstadter in Gödel, Escher, Bach: An Eternal Golden Braid) in DNA and signal the end of a protein sequence. More recently, the field of Evolutionary Developmental Biology (a.k.a. evo-devo) has encouraged this view:
“The field is characterized by some key concepts, which took biologists by surprise. One is deep homology, the finding that dissimilar organs such as the eyes of insects, vertebrates and cephalopod mollusks, long thought to have evolved separately, are controlled by similar genes such as pax-6, from the evo-devo gene toolkit. These genes are ancient, being highly conserved among phyla; they generate the patterns in time and space which shape the embryo, and ultimately form the body plan of the organism. Another is that species do not differ much in their structural genes, such as those coding for enzymes; what does differ is the way that gene expression is regulated by the toolkit genes. These genes are reused, unchanged, many times in different parts of the embryo and at different stages of development, forming a complex cascade of control, switching other regulatory genes as well as structural genes on and off in a precise pattern. This multiple pleiotropic reuse explains why these genes are highly conserved, as any change would have many adverse consequences which natural selection would oppose.
New morphological features and ultimately new species are produced by variations in the toolkit, either when genes are expressed in a new pattern, or when toolkit genes acquire additional functions. Another possibility is the Neo-Lamarckian theory that epigenetic changes are later consolidated at gene level, something that may have been important early in the history of multicellular life.” – from Wikipedia
Inspired by von Neuman and the developments of evo-devo, Gregory Chaitin in 2010 published a paper entitled “To a Mathematical Theory of Evolution and Biological Creativity“. Chaitin characterized DNA as a software program. He built a toy-model of evolution where computer algorithms would compute the busy beaver problem of mathematics. In this problem, he tries to get the computer program to generate the biggest integer it can. Like children competitively yelling out larger and larger numbers: “I’m a million times stronger than you! Well, I’m a billion times stronger. No, I’m a billion, billion times. That’s nothing, I’m a billion to the billionth power times stronger!” – we get the idea. Simple as that. The program has no concept of infinity and so that’s off limits. There is a subroutine that randomly “mutates” the code at each generation. If the mutated code computes a bigger integer, it becomes the de facto code, otherwise it is thrown out (natural selection). Lots of times the mutated code just doesn’t work, or it enters a loop that never halts. So, an oracle is needed to supervise the development of the fledgling algorithms. It is a very interesting first look at DNA as an ancient programming language and an evolving algorithm. See his book, Proving Darwin: Making Biology Mathematical, for more.

Figure 8: Graph of variation in estimated genome sizes in base pairs (bp). Graph and caption by Abizar at Wikipedia
One thing is for certain: the incredible compactness of DNA molecules implies it has learned an enormous amount of information about the construction of biological organisms. Physicist Richard Feynman famously said “what I cannot create, I do not understand.” Inferring from Feynman: since DNA can create life (maybe “build” is a better word), it therefore understands it. This is certainly part of the miracle of biological evolution – understanding the impact of genetic changes on the organism. The simple description of the organism embedded in DNA allows life to predictably estimate the consequences of genetic changes – it is the key to generalizing well. It is why adaptive mutations are so successful. It is why the hopeless monsters are missing! When embryos adapt to stress so successfully, it’s because life knows what it is doing. The information is embedded in the genetic code!

Figure 9: Video of an Octopus camouflaging itself. A dramatic demonstration of how DNA understands how to build organisms – it gives the Octopus this amazing toolkit! Turns out it has an MDL of only 3 basic textures and the chromatophores come in only 3 basic colors! – by SciFri with marine biologist Roger Hanlon
In terms of house blueprints, it means life is so well ordered that living “houses” are all modular. The rooms have such symmetry to them that the plumbing always goes in the same corner, the electrical wiring always lines up, the windows and doors work, even though the “houses” are incredibly complex! You can swap out the upstairs, replace it with the plans from another and everything will work. Change living rooms if you want, it will all work, total plug-and-play modular design. It is all because of this remarkably organized, simple MDL blueprint.
The trouble is: how did this understanding come to be in the first place? And, even understanding what mutations might successfully lead to adaptation to a stress, how does life initiate and coordinate the change among the billions of impacted molecules throughout the organism? Half of the secret sauce of machine learning was quantifying complexity and the other half was allowing creative intelligent beings, such as ourselves, to inject our domain knowledge into the learning algorithm. DNA should have no such benefit, or should it? Not only that, but recent evidence suggests the role of epigenetic factors, such as methylation of DNA, is significant in heredity. How does DNA understand the impact of methylation? Where is this information stored? Seemingly not in the DNA, but if not, then where?